Divide and Conquer

                    Divide and Conquer


Introduction to Divide and Conquer

Divide and conquer (D&C) is an algorithm design paradigm based on multi-branched recursion. A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same type, until these become simple enough to be solved directly. The solutions to the sub-problems are then combined to give a solution to the original problem. A typical Divide and Conquer algorithm solves a problem using following three steps.

1. Divide: Break the problem into sub-problems of same type.
2. Conquer: Recursively solve these sub-problems.
3. Combine: Combine the solution sub-problems.

For Example: Assuming that each divide step creates two sub-problems



If we can divide the problem into more than two, it looks like this:



2. Standard Algorithms based on Divide and Conquer

The following algorithms are based on divide-and-conquer algorithm design paradigm −

Merge Sort

Quick Sort

Binary Search

Strassen's Matrix Multiplication

Closest pair (points)

Cooley–Tukey Fast Fourier Transform (FFT) algorithm

Karatsuba algorithm for fast multiplication

3. Advantages of Divide and Conquer

The most recognizable benefit of the divide and conquer paradigm is that it allows us to solve difficult problem, such as the Tower of Hanoi, which is a mathematical game or puzzle. Being given a difficult problem can often be discouraging if there is no idea how to go about solving it. However, with the divide and conquer method, it reduces the degree of difficulty since it divides the problem into sub problems that are easily solvable, and usually runs faster than other algorithms would.

It also uses memory caches effectively. When the sub problems become simple enough, they can be solved within a cache, without having to access the slower main memory.

4. Disadvantages of Divide and Conquer

One of the most common issues with this sort of algorithm is the fact that the recursion is slow, which in some cases outweighs any advantages of this divide and conquer process.

Sometimes it can become more complicated than a basic iterative approach, especially in cases with a large n.
In other words, if someone wanted to add a large amount of numbers together, if they just create a simple loop to add them together, it would turn out to be a much simpler approach than it would be to divide the numbers up into two groups, add these groups recursively, and then add the sums of the two groups together

Implementation of Divide and Conquer

In Divide and Conquer, we generally deal with arrays and our task is to first divide the array into smaller subarrays.



At first, it might seem that we are going to make new smaller subarrays for this purpose but this is not the case. Suppose we have to divide an array into two subarrays, we would introduce a variable which will point to the element from which we are breaking the array.



So, now we will deal with the array from 'start' to 'middle' as one smaller array and the array from 'middle+1' to 'end' as the second subarray.

Let's take an array and write a program to break it into a smaller subarrays of size 1 as shown in the first picture. We are first breaking the array into two subarrays and then again breaking those arrays into 4 subarrays and so on. So, it looks like a process of breaking an array into two halves and then repeatedly applying this process to smaller arrays to again break them in two halves.



Thus, we can make a function for the process of breaking the array and then recursively pass smaller arrays to it.

Let's write a function which breaks an array into smaller arrays and when the size of smaller array reaches to 1, it increases their value by 1.



As discussed above, we are not going to make any new arrays for smaller arrays, instead, we will use variables to divide the array. It means that our function should only treat the region marked by the variables as an array and that is how we will break the array. So, we will use two variables 'start' and 'end' to represent an array. Even if the array is bigger than whatever is enclosed in 'start' and 'end', inside the function, only this region will be treated as the array.



So, let's start writing the function - DEMO(A, start, end) → 'DEMO' is the name of the function, 'A' is the array passed to it and 'start' and 'end' are the starting and the ending indices respectively.

We will break the array from the middle element but this is always not the case. For example, some algorithms require to break the array from a specific pivot point like the median, a random element, etc. So, we just need to calculate the middle element i.e., ⌊(start+end)/2⌋⌊(start+end)/2⌋.

Now, we want the array to be broken from this middle element. To do this, we will simply pass the array to the function again but this time once we will pass array with starting index 'start' and ending index 'middle' and again with the starting index 'middle+1' and ending index 'end' i.e., DEMO(A, start, middle) and DEMO(A, middle+1, end).



So, we have broken our array and this function will again break the array into even smaller subarrays.





Now, this should stop when the subarray reaches the size of 1, and in that case, the 'start' and the 'end' will point to the same element. So, we will call DEMO(A, start, middle) and DEMO(A, middle+1, end) only when the 'start' is less than the 'right' because if they are equal then the array has only one element in it and there is no need of further breaking it.

DEMO(A, start, end)
  if start < right
    middle = floor((start+end)/2)
    DEMO(A, start, middle)
    DEMO(A, middle+1, end)

And thus, we are done with the dividing part. Now let's focus on the conquer part, and here we have to increase the value of each element by 1. We can easily do this after reaching the base case i.e. when 'start' is not less than 'end', we will increase the value of the element by 1 A[start] = A[start]+1.

DEMO(A, start, end)
  if start < right
    ...
  else
    A[start] = A[start]+1

Program for Divide and conquer

Binary Search

Till now, we have studied two sorting algorithms which implemented the Divide and Conquer technique. Binary search is a searching algorithm which uses the Divide and Conquer technique to perform search on a sorted data.

Normally, we iterate over an array to find if an element is present in an array or not. But think about a case when the data which we are provided is a sorted one, then performing a normal search will do the work but shouldn't we extract something useful from the fact that our data is already sorted?

So, let's have a look at the working of the binary search and find out how to perform an optimized search on a sorted data.

Working of Binary Search

In binary search, we directly hit the middle element and then compare it with the element to be found.



If the element to be found is equal to the middle element, then we have already found the element, otherwise, if it is smaller, then we know it is going to lie on the left side of it, else, on the right.



Let's take the case when the element to be found is smaller than the middle element, then we will repeat the same procedure on the left subarray by hitting the middle element of the left subarray.





So, this is how binary search works. But before discussing the code of the binary search let's first compare binary search with the traditional search.


Coding Binary Search

Our function is going to take an array, starting index, ending index and the element to be searched (x). So, we can declare the function for the binary search as BINARY-SEARCH(A, start, end, x).

We start by hitting the middle element, so let's start by calculating the middle element first i.e., middle = floor((start+end)/2).

Now, we have to compare this element with the element to be searched and if the element to be searched is the middle element, then we end up the function by returning its index i.e.,

if A[middle]==x
  return middle

If the element is smaller than the middle element, then we will repeat the binary search in the left subarray.

if A[middle]>x
  return BINARY-SEARCH(A, start, middle-1)

Similarly, we will repeat with the right subarray if the element to be found is greater than the middle element.

if A[middle]<x
  return BINARY-SEARCH(A, middle+1, end)

Thus, the entire code for the binary search can be written as:

BINARY-SEARCH(A, start, end, x) if start <= end middle = floor((start+end)/2) if A[middle]==x return middle if A[middle]>x return BINARY-SEARCH(A, start, middle-1, x) if A[middle]<x return BINARY-SEARCH(A, middle+1, end, x) return FALSE // in case, element is


Program for binary search

#include <stdio.h>
int binary_search(int a[], int start, int end, int x)
{
if(start <= end) { int middle = (start+end)/2; if(a[middle] == x)
 {
return middle;
}
 if(a[middle] > x)
{ return binary_search(a, start, middle-1, x);
 }
if(a[middle] < x)
 {
return binary_search(a, middle+1, end, x);
}
}
return -1; // not found
}
 int main()
{
 int a[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int index_result = binary_search(a, 0, 9, 7); printf("%d\n",index_result);
 return 0;
 }

Merge Sort

Merge sort is the first algorithm we are going to study in Divide and Conquer. According to Divide and Conquer, it first divides an array into smaller subarrays and then merges them together to get a sorted array. The dividing part is the same as what we did in the previous chapter.



The real thing lies in the combining part. We combine the arrays back together in such a way that we get the sorted array. So, we will make two functions, one to break the arrays into subarrays and another to merge the smaller arrays together to get a sorted array. Let's start by making the first function which is similar to the function we made in the previous chapter.

MERGE-SORT(A, start, end)
  if start < right
    middle = floor((start+end)/2)
    MERGE-SORT(A, start, middle)
    MERGE-SORT(A, middle+1, end)

With this code, we will be able to break our array into smaller subarrays, but now we want the subarrays to combine together and make a sorted array. For this purpose, let's focus on writing the merge function.

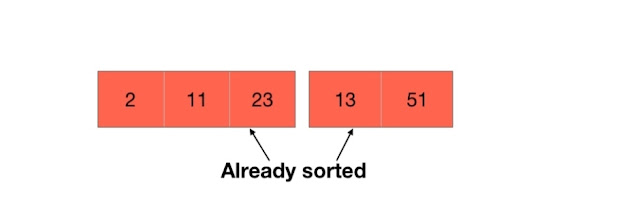
To merge the smaller arrays back together, we will start iterating over the arrays and putting the smaller element first to get a sorted array. This will be clear from the picture given below.



From the above picture, you can see that we are iterating over both the arrays simultaneously and comparing the elements and then putting the smaller element in the final array and then continuing the iteration. But one doubt can come in anyone's mind that both the arrays shown in the above picture are themselves sorted and then we are merging them together to get the final sorted array, so how are we going to get the two smaller arrays sorted?



The answer is simple, we are breaking our arrays into smaller subarrays until the size of each subarray becomes 1 and any array with just a single element is already sorted in itself. So, we will start merging them together to get bigger sorted arrays.


Since we are clear with the entire idea of Merge Sort, so let's write code for the merge function.

Code for Merge Sort

As shown in the picture above, the merge function is going to merge two arrays which are already sorted. However, these two arrays will not be entirely different arrays but a single array which will be separated by a variable into two arrays because this is how we are breaking our arrays.

So, our function to merge the arrays will take an array, starting index, ending index and the middle index from which the array is separated i.e., MERGE(A, start, middle, end).

Now, we have to iterate over both the subarrays, compare the elements and put the smaller one into the final array. But we don't have any final array to work with, all we have is a single array and the indices. So, let's copy the subarrays into two temporary arrays and modify the initial array 'A' to make it sorted.

So, our first task is to make two temporary arrays.

temp1 = A[start, middle]
temp2 = A[middle+1, end]

Now, we have to iterate over these arrays and compare the elements and then put the smaller elements into the bigger array.

i = 1
j = 1
k = start
while i <= temp1.length and j <= temp2.length
  if temp1[i] < temp2[j]
    A[k] = temp1[i]
    i=i+1
  else
    A[k] = temp2[j]
    j=j+1
  k=k+1

We are iterating over both the arrays with while i <= temp1.length and j <= temp2.length and then comparing the elements - if temp1[i] < temp2[j]. After that, we are putting the smaller element into the array first - A[k] = temp1[i] (if temp1 has smaller element) or A[k] = temp2[j] (if temp2 has smaller element) and then we are continuing our iteration with i = i+1 or j = j+1, which ever element was put to the array. At last, k = k+1 is making the increase for the iteration on the original array. The illustration for the same is given below.

One thing you can note from the above picture is that after this process, it might be possible that we are left with few elements in any of the subarrays. To handle this case, let's just copy the remaining elements to the array. Because these elements are already sorted and only the larger elements are going to be left, so direct copying is going to work for us.

while i < temp1.length
  A[k] = temp[i]
  i = i+1

while j < temp2.length
  A[k] = temp[j]
  j = j+1

The first while loop is iterating over the temp1 array and copying any leftover of the array. The second loop is doing the same thing but with the array temp2.

So, now we are ready to write the merge function.

MERGE(A, start, middle, end)
temp1 = A[start, middle]
temp2 = A[middle+1, end]
i = 1
j = 1
k = start
while i <= temp1.length and j <= temp2.length
if temp1[i] < temp2[j] A[k] = temp1[i]
 i=i+1
else
A[k] = temp2[j]
j=j+1
k=k+1
while i < temp1.length
A[k] = temp[i]
 i = i+1
 while j < temp2.length
A[k] = temp[j]
j = j+1

Now, we have to use this MERGE function inside the MERGE-SORT function which is basically dividing the array into subarrays. Till now, we have developed the MERGE-SORT function as:

MERGE-SORT(A, start, end)
  if start < right
    middle = floor((start+end)/2)
    MERGE-SORT(A, start, middle)
    MERGE-SORT(A, middle+1, end)







QuickSort

Quicksort is another sorting algorithm which uses Divide and Conquer for its implementation. Quicksort is also the practical choice of algorithm for sorting because of its good performance in the average case which is Θ(nlgn)Θ(nlg⁡n). Unlike the Merge Sort, Quicksort doesn't use any extra array in its sorting process and even if its average case is same as that of the Merge Sort, the hidden factors of Θ(nlgn)Θ(nlg⁡n) are generally smaller in the case of Quicksort.

So, Quicksort sounds like the perfect sorting algorithm we always needed, but hold on for a second, Quicksort is also not as perfect as it sounds. In the worst case, Quicksort gives us a quadratic (O(n2)O(n2)) performance which might be concerning in many cases. So, let's move forward and discuss in detail about Quicksort.

Quicksort first chooses a pivot and then partition the array around this pivot. In the partitioning process, all the elements smaller than the pivot are put on one side of the pivot and all the elements larger than it on the other side.



This partitioning process is repeated on the smaller subarrays and hence finally results in a sorted array.



So, let's first focus on making the partition function.

Partition in Quicksort

The first step of doing a partition is choosing a pivot. We are going to always select the last element of the array as the pivot in our algorithm and focus mainly on the concepts behind the Quicksort. However, there can be different ways of choosing the pivot like the median of the elements, the first element of the array, random element, etc.

After choosing the pivot, our next task is to place all the elements smaller than the pivot on one side and all the elements larger than the pivot on another side. We will do this by iterating over the array and on finding an element larger than the pivot, doing nothing. This will start making a cluster of elements larger than the pivot.

Now on finding any element smaller than the pivot, we will swap it with the first element of the cluster of the larger elements. In this way, we will start making another cluster of elements smaller than the pivot.



At last, we will swap the pivot with the first element of the cluster of the larger elements.





Thus, we have successfully done the partition of the array. So, let's write the code for the same.

Code for Partition in Quicksort

As stated above, this partition is going to repeatedly occur on smaller subarrays after dividing the array into subarrays. So, the function for partition is going to take an array, a starting index and an ending index i.e., PARTITION(A, start, end).

The next task is to make the pivot element. In our case, it is the last element i.e., pivot = A[end].

After this, we have to iterate over the array and check if the element is smaller or larger than the pivot and then swap it with the first element of the cluster of the larger elements. So, we will use a variable to know the first element of the cluster of the larger elements.

Initially, we will start our iteration by setting this pointer outside our array i.e., i = start-1 and this pointer will always point to the last element of the cluster of the smaller elements.



Whenever we will have a need to swap the elements, we will increase its value to point the first element of the cluster of the larger elements.



i = start-1
for j in start to end-1
  if A[j] <= pivot

Now, if the condition is true i.e., the element is smaller than the pivot, then we have to swap it with the first element of the cluster of the larger elements. So, we will increase the value of 'i' by 1 and then do the swapping.

for j in start to end-1
  if A[j] <= pivot
    i = i+1
    swap(A[i], A[j])

Thus, we are done with making the clusters and the only task left is to swap the pivot with the first element of the cluster of the larger elements.

for j in start to end-1
  if A[j] <= pivot
    ...
  swap(A[i+1], A[end]) // swapping pivot

One last thing we want from our PARTITION function is to return the index of the pivot, so we can then use this index to divide our array further into subarrays.

for j in start to end-1
  ...
  swap(A[i+1], A[end]) // swapping pivot
return i+1

That's it. We are done with the code to partition an array.

PARTITION(A, start, end) pivot = A[end] i = start-1 for j in start to end-1 if A[j] <= pivot i = i+1 swap(A[i], A[j]) swap(A[i+1], A[end]) //swapping pivot return i+1

Now we are done with the PARTITION function, so let's focus on repeating it to subarrays.

Code for Quicksort

From the previous two chapters, we already have been applying divide and conquer to break the array into subarrays but we were using the middle element to do so. In quicksort, we will use the index returned by the PARTITION function to do this.

Here also, we will continue breaking the array until the size of the array becomes 1 i.e., until start < end.

So, we will first start by partitioning our array i.e., q = PARTITION(A, start, end). 'q' is storing the index of the pivot here. After this, we will again repeat this process to the subarray from 'start' to 'q-1' and 'q+1' to 'end', leaving the pivot element because that is already in the place.



QUICKSORT(A, start, end)
 if start < end q = PARTITION(A, start, end) QUICKSORT(A, start, q-1)
QUICKSORT(A, q+1, end)

Strassen’s Matrix Multiplication in algorithms

In this article, we are going to discuss about the strassen matrix multiplication, formula of matrix multiplication and algorithms for strassen matrix multiplication.
Submitted by Prerana Jain, on June 22, 2018

Introduction

Strassen in 1969 which gives an overview that how we can find the multiplication of two 2*2 dimension matrix by the brute-force algorithm. But by using divide and conquer technique the overall complexity for multiplication two matrices is reduced. This happens by decreasing the total number if multiplication performed at the expenses of a slight increase in the number of addition.

For multiplying the two 2*2 dimension matrices Strassen's used some formulas in which there are seven multiplication and eighteen addition, subtraction, and in brute force algorithm, there is eight multiplication and four addition. The utility of Strassen's formula is shown by its asymptotic superiority when order n of matrix reaches infinity. Let us consider two matrices A and B, n*n dimension, where n is a power of two. It can be observed that we can contain four n/2*n/2 submatrices from A, B and their product C. C is the resultant matrix of A and B.

Procedure of Strassen matrix multiplication

There are some procedures:

Divide a matrix of order of 2*2 recursively till we get the matrix of 2*2.

Use the previous set of formulas to carry out 2*2 matrix multiplication.

In this eight multiplication and four additions, subtraction are performed.

Combine the result of two matrixes to find the final product or final matrix.

Formulas for Stassen’s matrix multiplication

In Strassen’s matrix multiplication there are seven multiplication and four addition, subtraction in total.

1. D1 = (a11 + a22) (b11 + b22)
2. D2 = (a21 + a22).b11
3. D3 = (b12 – b22).a11
4. D4 = (b21 – b11).a22
5. D5 = (a11 + a12).b22
6. D6 = (a21 – a11) . (b11 + b12)
7. D7 = (a12 – a22) . (b21 + b22)
C11 = d1 + d4 – d5 + d7
C12 = d3 + d5
C21 = d2 + d4
C22 = d1 + d3 – d2 – d6

Algorithm for Strassen’s matrix multiplication

Algorithm Strassen(n, a, b, d)

begin If n = threshold then compute
C = a * b is a conventional matrix.
Else
Partition a into four sub matrices a11, a12, a21, a22.
Partition b into four sub matrices b11, b12, b21, b22.
Strassen ( n/2, a11 + a22, b11 + b22, d1) Strassen ( n/2, a21 + a22, b11, d2)
Strassen ( n/2, a11, b12 – b22, d3)
Strassen ( n/2, a22, b21 – b11, d4)
Strassen ( n/2, a11 + a12, b22, d5)
Strassen (n/2, a21 – a11, b11 + b22, d6) Strassen (n/2, a12 – a22, b21 + b22, d7)
C = d1+d4-d5+d7                           d3+d5 d2+d4             d1+d3-d2-d6
end if
return (C) end.

Code for Strassen matrix multiplication

#include <stdio.h>

int main()
{
int a[2][2],b[2][2],c[2][2],i,j;
int m1,m2,m3,m4,m5,m6,m7;

printf("Enter the 4 elements of first matrix: ");
for(i=0;i<2;i++)
for(j=0;j<2;j++)
scanf("%d",&a[i][j]);

printf("Enter the 4 elements of second matrix: ");
for(i=0;i<2;i++)
for(j=0;j<2;j++)
scanf("%d",&b[i][j]);

printf("\nThe first matrix is\n");
for(i=0;i<2;i++)
{
printf("\n");
for(j=0;j<2;j++)
printf("%d\t",a[i][j]);
}

printf("\nThe second matrix is\n");
for(i=0;i<2;i++)
{
printf("\n");
for(j=0;j<2;j++)
printf("%d\t",b[i][j]);
}

m1= (a[0][0] + a[1][1])*(b[0][0]+b[1][1]);
m2= (a[1][0]+a[1][1])*b[0][0];
m3= a[0][0]*(b[0][1]-b[1][1]);
m4= a[1][1]*(b[1][0]-b[0][0]);
m5= (a[0][0]+a[0][1])*b[1][1];
m6= (a[1][0]-a[0][0])*(b[0][0]+b[0][1]);
m7= (a[0][1]-a[1][1])*(b[1][0]+b[1][1]);

c[0][0]=m1+m4-m5+m7;
c[0][1]=m3+m5;
c[1][0]=m2+m4;
c[1][1]=m1-m2+m3+m6;

printf("\nAfter multiplication using \n");
for(i=0;i<2;i++)
{
printf("\n");
for(j=0;j<2;j++)
printf("%d\t",c[i][j]);
}

return 0;
}

Output

Enter the 4 elements of first matrix: 5

6
7
8
Enter the 4 elements of second matrix: 1
2
3
4

The first matrix is

5       6
7       8
The second matrix is

1       2
3       4
After multiplication using

23      34
31      46