NP Completeness
NP Completeness
Introduction
We have been writing about efficient algorithms to solve complex problems, like shortest path, Euler graph, minimum spanning tree, etc. Those were all success stories of algorithm designers. In this post, failure stories of computer science are discussed.
Can all computational problems be solved by a computer? There are computational problems that can not be solved by algorithms even with unlimited time. For example Turing Halting problem (Given a program and an input, whether the program will eventually halt when run with that input, or will run forever). Alan Turing proved that general algorithm to solve the halting problem for all possible program-input pairs cannot exist. A key part of the proof is, Turing machine was used as a mathematical definition of a computer and program (Source Halting Problem).
Status of NP Complete problems is another failure story, NP complete problems are problems whose status is unknown. No polynomial time algorithm has yet been discovered for any NP complete problem, nor has anybody yet been able to prove that no polynomial-time algorithm exist for any of them. The interesting part is, if any one of the NP complete problems can be solved in polynomial time, then all of them can be solved.
Status of NP Complete problems is another failure story, NP complete problems are problems whose status is unknown. No polynomial time algorithm has yet been discovered for any NP complete problem, nor has anybody yet been able to prove that no polynomial-time algorithm exist for any of them. The interesting part is, if any one of the NP complete problems can be solved in polynomial time, then all of them can be solved.
What are NP, P, NP-complete and NP-Hard problems?
P is set of problems that can be solved by a deterministic Turing machine in Polynomial time.
P is set of problems that can be solved by a deterministic Turing machine in Polynomial time.
NP is set of decision problems that can be solved by a Non-deterministic Turing Machine in Polynomial time. P is subset of NP (any problem that can be solved by deterministic machine in polynomial time can also be solved by non-deterministic machine in polynomial time).
Informally, NP is set of decision problems which can be solved by a polynomial time via a “Lucky Algorithm”, a magical algorithm that always makes a right guess among the given set of choices (Source Ref 1).
Informally, NP is set of decision problems which can be solved by a polynomial time via a “Lucky Algorithm”, a magical algorithm that always makes a right guess among the given set of choices (Source Ref 1).
NP-complete problems are the hardest problems in NP set. A decision problem L is NP-complete if:
1) L is in NP (Any given solution for NP-complete problems can be verified quickly, but there is no efficient known solution).
2) Every problem in NP is reducible to L in polynomial time (Reduction is defined below).
1) L is in NP (Any given solution for NP-complete problems can be verified quickly, but there is no efficient known solution).
2) Every problem in NP is reducible to L in polynomial time (Reduction is defined below).
A problem is NP-Hard if it follows property 2 mentioned above, doesn’t need to follow property 1. Therefore, NP-Complete set is also a subset of NP-Hard set.
Decision vs Optimization Problems
NP-completeness applies to the realm of decision problems. It was set up this way because it’s easier to compare the difficulty of decision problems than that of optimization problems. In reality, though, being able to solve a decision problem in polynomial time will often permit us to solve the corresponding optimization problem in polynomial time (using a polynomial number of calls to the decision problem). So, discussing the difficulty of decision problems is often really equivalent to discussing the difficulty of optimization problems. (Source Ref 2).
For example, consider the vertex cover problem (Given a graph, find out the minimum sized vertex set that covers all edges). It is an optimization problem. Corresponding decision problem is, given undirected graph G and k, is there a vertex cover of size k?
NP-completeness applies to the realm of decision problems. It was set up this way because it’s easier to compare the difficulty of decision problems than that of optimization problems. In reality, though, being able to solve a decision problem in polynomial time will often permit us to solve the corresponding optimization problem in polynomial time (using a polynomial number of calls to the decision problem). So, discussing the difficulty of decision problems is often really equivalent to discussing the difficulty of optimization problems. (Source Ref 2).
For example, consider the vertex cover problem (Given a graph, find out the minimum sized vertex set that covers all edges). It is an optimization problem. Corresponding decision problem is, given undirected graph G and k, is there a vertex cover of size k?
What is Reduction?
Let L1 and L2 be two decision problems. Suppose algorithm A2 solves L2. That is, if y is an input for L2 then algorithm A2 will answer Yes or No depending upon whether y belongs to L2 or not.
The idea is to find a transformation from L1 to L2 so that the algorithm A2 can be part of an algorithm A1 to solve L1.
Learning reduction in general is very important. For example, if we have library functions to solve certain problem and if we can reduce a new problem to one of the solved problems, we save a lot of time. Consider the example of a problem where we have to find minimum product path in a given directed graph where product of path is multiplication of weights of edges along the path. If we have code for Dijkstra’s algorithm to find shortest path, we can take log of all weights and use Dijkstra’s algorithm to find the minimum product path rather than writing a fresh code for this new problem.
Let L1 and L2 be two decision problems. Suppose algorithm A2 solves L2. That is, if y is an input for L2 then algorithm A2 will answer Yes or No depending upon whether y belongs to L2 or not.
The idea is to find a transformation from L1 to L2 so that the algorithm A2 can be part of an algorithm A1 to solve L1.
Learning reduction in general is very important. For example, if we have library functions to solve certain problem and if we can reduce a new problem to one of the solved problems, we save a lot of time. Consider the example of a problem where we have to find minimum product path in a given directed graph where product of path is multiplication of weights of edges along the path. If we have code for Dijkstra’s algorithm to find shortest path, we can take log of all weights and use Dijkstra’s algorithm to find the minimum product path rather than writing a fresh code for this new problem.
How to prove that a given problem is NP complete?
From the definition of NP-complete, it appears impossible to prove that a problem L is NP-Complete. By definition, it requires us to that show every problem in NP is polynomial time reducible to L. Fortunately, there is an alternate way to prove it. The idea is to take a known NP-Complete problem and reduce it to L. If polynomial time reduction is possible, we can prove that L is NP-Complete by transitivity of reduction (If a NP-Complete problem is reducible to L in polynomial time, then all problems are reducible to L in polynomial time).
From the definition of NP-complete, it appears impossible to prove that a problem L is NP-Complete. By definition, it requires us to that show every problem in NP is polynomial time reducible to L. Fortunately, there is an alternate way to prove it. The idea is to take a known NP-Complete problem and reduce it to L. If polynomial time reduction is possible, we can prove that L is NP-Complete by transitivity of reduction (If a NP-Complete problem is reducible to L in polynomial time, then all problems are reducible to L in polynomial time).
What was the first problem proved as NP-Complete?
There must be some first NP-Complete problem proved by definition of NP-Complete problems. SAT (Boolean satisfiability problem) is the first NP-Complete problem proved by Cook (See CLRS book for proof).
There must be some first NP-Complete problem proved by definition of NP-Complete problems. SAT (Boolean satisfiability problem) is the first NP-Complete problem proved by Cook (See CLRS book for proof).
It is always useful to know about NP-Completeness even for engineers. Suppose you are asked to write an efficient algorithm to solve an extremely important problem for your company. After a lot of thinking, you can only come up exponential time approach which is impractical. If you don’t know about NP-Completeness, you can only say that I could not come with an efficient algorithm. If you know about NP-Completeness and prove that the problem as NP-complete, you can proudly say that the polynomial time solution is unlikely to exist. If there is a polynomial time solution possible, then that solution solves a big problem of computer science many scientists have been trying for years.
We will soon be discussing more NP-Complete problems and their proof for NP-Completeness.
Polynomial Time Verification
Before talking about the class of NP-complete problems, it is essential to introduce the notion of a verification algorithm.
Many problems are hard to solve, but they have the property that it easy to authenticate the solution if one is provided.
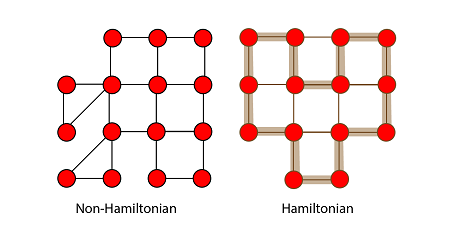
Hamiltonian cycle problem:-
Consider the Hamiltonian cycle problem. Given an undirected graph G, does G have a cycle that visits each vertex exactly once? There is no known polynomial time algorithm for this dispute.
Note: - It means you can't build a Hamiltonian cycle in a graph with a polynomial time even if there is no specific path is given for the Hamiltonian cycle with the particular vertex, yet you can't verify the Hamiltonian cycle within the polynomial time

Fig: Hamiltonian Cycle
Let us understand that a graph did have a Hamiltonian cycle. It would be easy for someone to convince of this. They would similarly say: "the period is hv3, v7, v1....v13i.
We could then inspect the graph and check that this is indeed a legal cycle and that it visits all of the vertices of the graph exactly once. Thus, even though we know of no efficient way to solve the Hamiltonian cycle problem, there is a beneficial way to verify that a given cycle is indeed a Hamiltonian cycle.
Note:-For the verification in the Polynomial-time of an undirected Hamiltonian cycle graph G. There must be exact/specific/definite path must be given of Hamiltonian cycle then you can verify in the polynomial time.
Definition of Certificate: - A piece of information which contains in the given path of a vertex is known as certificate
Relation of P and NP classes
- P contains in NP
- P=NP
- Observe that P contains in NP. In other words, if we can solve a problem in polynomial time, we can indeed verify the solution in polynomial time. More formally, we do not need to see a certificate (there is no need to specify the vertex/intermediate of the specific path) to solve the problem; we can explain it in polynomial time anyway.
- However, it is not known whether P = NP. It seems you can verify and produce an output of the set of decision-based problems in NP classes in a polynomial time which is impossible because according to the definition of NP classes you can verify the solution within the polynomial time. So this relation can never be held.
Reductions:
The class NP-complete (NPC) problems consist of a set of decision problems (a subset of class NP) that no one knows how to solve efficiently. But if there were a polynomial solution for even a single NP-complete problem, then every problem in NPC will be solvable in polynomial time. For this, we need the concept of reductions.
Suppose there are two problems, A and B. You know that it is impossible to solve problem A in polynomial time. You want to prove that B cannot be explained in polynomial time. We want to show that (A ∉ P) => (B ∉ P)
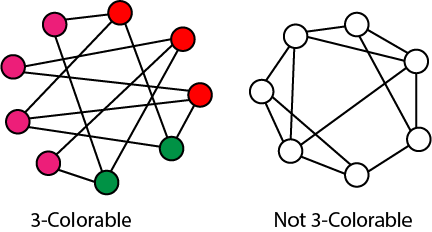
Consider an example to illustrate reduction: The following problem is well-known to be NPC:
3-color: Given a graph G, can each of its vertices be labeled with one of 3 different colors such that two adjacent vertices do not have the same label (color).
Coloring arises in various partitioning issues where there is a constraint that two objects cannot be assigned to the same set of partitions. The phrase "coloring" comes from the original application which was in map drawing. Two countries that contribute a common border should be colored with different colors.
It is well known that planar graphs can be colored (maps) with four colors. There exists a polynomial time algorithm for this. But deciding whether this can be done with 3 colors is hard, and there is no polynomial time algorithm for it.

Fig: Example of 3-colorable and non-3-colorable graphs.
Polynomial Time Reduction:
We say that Decision Problem L1 is Polynomial time Reducible to decision Problem L2 (L1≤p L2) if there is a polynomial time computation function f such that of all x, xϵL1 if and only if xϵL2.
Definition of Polynomial time: - If we produce an output according to the given input within a specific amount of time such as within a minute, hours. This is known as Polynomial time.
Definition of Non-Polynomial time: - If we produce an output according to the given input but there are no time constraints is known as Non-Polynomial time. But yes output will produce but time is not fixed yet.
Definition of Decision Based Problem: - A problem is called a decision problem if its output is a simple "yes" or "no" (or you may need this of this as true/false, 0/1, accept/reject.) We will phrase many optimization problems as decision problems. For example, Greedy method, D.P., given a graph G= (V, E) if there exists any Hamiltonian cycle.
Definition of NP-hard class: - Here you to satisfy the following points to come into the division of NP-hard
Definition of NP-complete class: - A problem is in NP-complete, if
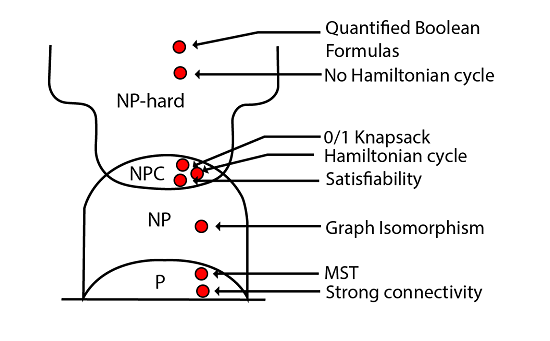
Fig: Complexity Classes
Thank you,
By Er. Shejwal Shrikant.
30-12-2019, Monday.
Complexity Classes
Definition of NP class Problem: - The set of all decision-based problems came into the division of NP Problems who can't be solved or produced an output within polynomial time but verified in the polynomial time. NP class contains P class as a subset. NP problems being hard to solve.Note: - The term "NP" does not mean "not polynomial." Originally, the term meant "non-deterministic polynomial. It means according to the one input number of output will be produced.
Definition of P class Problem: - The set of decision-based problems come into the division of P Problems who can be solved or produced an output within polynomial time. P problems being easy to solveDefinition of Polynomial time: - If we produce an output according to the given input within a specific amount of time such as within a minute, hours. This is known as Polynomial time.
Definition of Non-Polynomial time: - If we produce an output according to the given input but there are no time constraints is known as Non-Polynomial time. But yes output will produce but time is not fixed yet.
Definition of NP-hard class: - Here you to satisfy the following points to come into the division of NP-hard
- If we can solve this problem in polynomial time, then we can solve all NP problems in polynomial time
- If you convert the issue into one form to another form within the polynomial time
- It is in NP
- It is NP-hard

Fig: Complexity Classes
Thank you,
By Er. Shejwal Shrikant.
30-12-2019, Monday.


Comments
Post a Comment