Backtracking
Backtracking
Backtracking Concept
Backtracking is an algorithmic-technique for solving problems recursively by trying to build a solution incrementally, one piece at a time, removing those solutions that fail to satisfy the constraints of the problem at any point of time (by time, here, is referred to the time elapsed till reaching any level of the search tree).
For example, consider the SudoKo solving Problem, we try filling digits one by one. Whenever we find that current digit cannot lead to a solution, we remove it (backtrack) and try next digit. This is better than naive approach (generating all possible combinations of digits and then trying every combination one by one) as it drops a set of permutations whenever it backtracks.
1. N Queen Problem
The expected output is a binary matrix which has 1s for the blocks where queens are placed. For example, following is the output matrix for above 4 queen solution.
{ 0, 1, 0, 0}
{ 0, 0, 0, 1}
{ 1, 0, 0, 0}
{ 0, 0, 1, 0}
We have discussed Knight’s tour and Rat in a Maze problems in Set 1 and Set 2 respectively. Let us discuss N Queen as another example problem that can be solved using Backtracking.
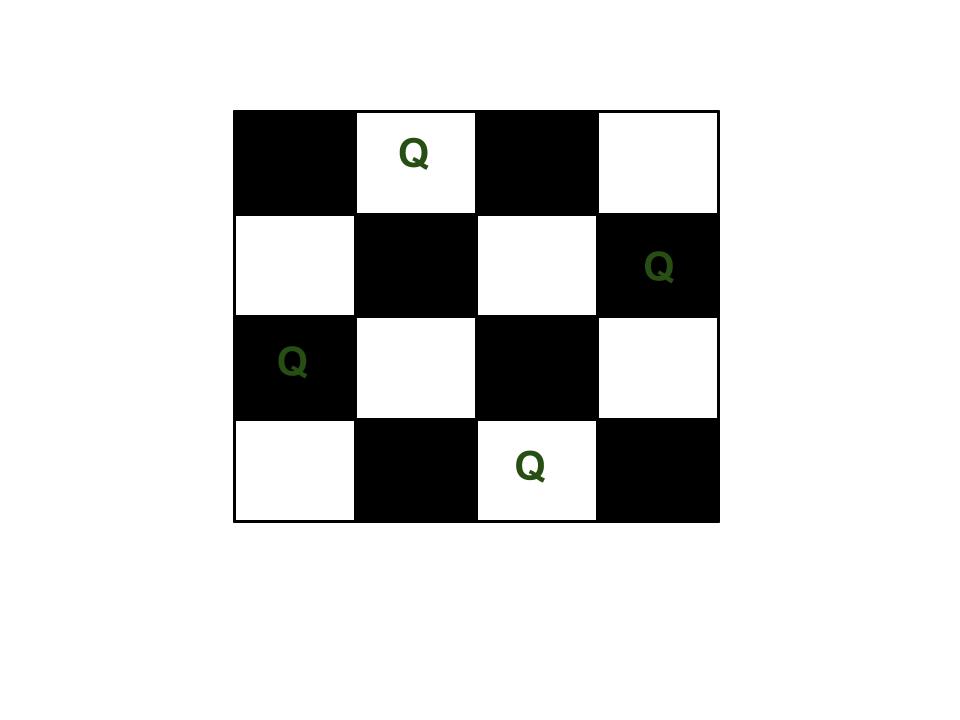
The N Queen is the problem of placing N chess queens on an N×N chessboard so that no two queens attack each other. For example, following is a solution for 4 Queen problem.
The expected output is a binary matrix which has 1s for the blocks where queens are placed. For example, following is the output matrix for above 4 queen solution.
{ 0, 1, 0, 0}
{ 0, 0, 0, 1}
{ 1, 0, 0, 0}
{ 0, 0, 1, 0}
Recommended: Please solve it on “PRACTICE ” first, before moving on to the solution.
Naive Algorithm
Generate all possible configurations of queens on board and print a configuration that satisfies the given constraints.
while there are untried configurations
{
generate the next configuration
if queens don't attack in this configuration then
{
print this configuration;
}
}
Backtracking Algorithm
The idea is to place queens one by one in different columns, starting from the leftmost column. When we place a queen in a column, we check for clashes with already placed queens. In the current column, if we find a row for which there is no clash, we mark this row and column as part of the solution. If we do not find such a row due to clashes then we backtrack and return false.
1) Start in the leftmost column
2) If all queens are placed
return true
3) Try all rows in the current column.
Do following for every tried row.
a) If the queen can be placed safely in this row
then mark this [row, column] as part of the
solution and recursively check if placing
queen here leads to a solution.
b) If placing the queen in [row, column] leads to
a solution then return true.
c) If placing queen doesn't lead to a solution then
unmark this [row, column] (Backtrack) and go to
step (a) to try other rows.
3) If all rows have been tried and nothing worked,
return false to trigger backtracking
Naive Algorithm
Generate all possible configurations of queens on board and print a configuration that satisfies the given constraints.
Generate all possible configurations of queens on board and print a configuration that satisfies the given constraints.
while there are untried configurations
{
generate the next configuration
if queens don't attack in this configuration then
{
print this configuration;
}
}
Backtracking Algorithm
The idea is to place queens one by one in different columns, starting from the leftmost column. When we place a queen in a column, we check for clashes with already placed queens. In the current column, if we find a row for which there is no clash, we mark this row and column as part of the solution. If we do not find such a row due to clashes then we backtrack and return false.
The idea is to place queens one by one in different columns, starting from the leftmost column. When we place a queen in a column, we check for clashes with already placed queens. In the current column, if we find a row for which there is no clash, we mark this row and column as part of the solution. If we do not find such a row due to clashes then we backtrack and return false.
1) Start in the leftmost column
2) If all queens are placed
return true
3) Try all rows in the current column.
Do following for every tried row.
a) If the queen can be placed safely in this row
then mark this [row, column] as part of the
solution and recursively check if placing
queen here leads to a solution.
b) If placing the queen in [row, column] leads to
a solution then return true.
c) If placing queen doesn't lead to a solution then
unmark this [row, column] (Backtrack) and go to
step (a) to try other rows.
3) If all rows have been tried and nothing worked,
return false to trigger backtracking
2.Hamiltonian Cycle
Hamiltonian Path in an undirected graph is a path that visits each vertex exactly once. A Hamiltonian cycle (or Hamiltonian circuit) is a Hamiltonian Path such that there is an edge (in the graph) from the last vertex to the first vertex of the Hamiltonian Path. Determine whether a given graph contains Hamiltonian Cycle or not. If it contains, then prints the path. Following are the input and output of the required function.
Input:
A 2D array graph[V][V] where V is the number of vertices in graph and graph[V][V] is adjacency matrix representation of the graph. A value graph[i][j] is 1 if there is a direct edge from i to j, otherwise graph[i][j] is 0.
A 2D array graph[V][V] where V is the number of vertices in graph and graph[V][V] is adjacency matrix representation of the graph. A value graph[i][j] is 1 if there is a direct edge from i to j, otherwise graph[i][j] is 0.
Output:
An array path[V] that should contain the Hamiltonian Path. path[i] should represent the ith vertex in the Hamiltonian Path. The code should also return false if there is no Hamiltonian Cycle in the graph.
An array path[V] that should contain the Hamiltonian Path. path[i] should represent the ith vertex in the Hamiltonian Path. The code should also return false if there is no Hamiltonian Cycle in the graph.
For example, a Hamiltonian Cycle in the following graph is {0, 1, 2, 4, 3, 0}.
(0)--(1)--(2) | / \ | | / \ | | / \ | (3)-------(4)
And the following graph doesn’t contain any Hamiltonian Cycle.
(0)--(1)--(2) | / \ | | / \ | | / \ | (3) (4)
Naive Algorithm
Generate all possible configurations of vertices and print a configuration that satisfies the given constraints. There will be n! (n factorial) configurations.
Generate all possible configurations of vertices and print a configuration that satisfies the given constraints. There will be n! (n factorial) configurations.
while there are untried conflagrations
{
generate the next configuration
if ( there are edges between two consecutive vertices of this
configuration and there is an edge from the last vertex to
the first ).
{
print this configuration;
break;
}
}
Backtracking Algorithm
Create an empty path array and add vertex 0 to it. Add other vertices, starting from the vertex 1. Before adding a vertex, check for whether it is adjacent to the previously added vertex and not already added. If we find such a vertex, we add the vertex as part of the solution. If we do not find a vertex then we return false.
Create an empty path array and add vertex 0 to it. Add other vertices, starting from the vertex 1. Before adding a vertex, check for whether it is adjacent to the previously added vertex and not already added. If we find such a vertex, we add the vertex as part of the solution. If we do not find a vertex then we return false.
Implementation of Backtracking solution
Following are implementations of the Backtracking solution.
Following are implementations of the Backtracking solution.
C
Output:
Solution Exists: Following is one Hamiltonian Cycle 0 1 2 4 3 0 Solution does not exist
Note that the above code always prints cycle starting from 0. The starting point should not matter as the cycle can be started from any point. If you want to change the starting point, you should make two changes to the above code.
Change “path[0] = 0;” to “path[0] = s;” where s is your new starting point. Also change loop “for (int v = 1; v < V; v++)" in hamCycleUtil() to "for (int v = 0; v < V; v++)".
Change “path[0] = 0;” to “path[0] = s;” where s is your new starting point. Also change loop “for (int v = 1; v < V; v++)" in hamCycleUtil() to "for (int v = 0; v < V; v++)".
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
3. Subset Sum
Subset sum problem is to find subset of elements that are selected from a given set whose sum adds up to a given number K. We are considering the set contains non-negative values. It is assumed that the input set is unique (no duplicates are presented).
Exhaustive Search Algorithm for Subset Sum
One way to find subsets that sum to K is to consider all possible subsets. A power set contains all those subsets generated from a given set. The size of such a power set is 2N.
Backtracking Algorithm for Subset Sum
Using exhaustive search we consider all subsets irrespective of whether they satisfy given constraints or not. Backtracking can be used to make a systematic consideration of the elements to be selected.
Assume given set of 4 elements, say w[1] … w[4]. Tree diagrams can be used to design backtracking algorithms. The following tree diagram depicts approach of generating variable sized tuple.
In the above tree, a node represents function call and a branch represents candidate element. The root node contains 4 children. In other words, root considers every element of the set as different branch. The next level sub-trees correspond to the subsets that includes the parent node. The branches at each level represent tuple element to be considered. For example, if we are at level 1, tuple_vector[1] can take any value of four branches generated. If we are at level 2 of left most node, tuple_vector[2] can take any value of three branches generated, and so on…
For example the left most child of root generates all those subsets that include w[1]. Similarly the second child of root generates all those subsets that includes w[2] and excludes w[1].
As we go down along depth of tree we add elements so far, and if the added sum is satisfying explicit constraints, we will continue to generate child nodes further. Whenever the constraints are not met, we stop further generation of sub-trees of that node, and backtrack to previous node to explore the nodes not yet explored. In many scenarios, it saves considerable amount of processing time.
The tree should trigger a clue to implement the backtracking algorithm (try yourself). It prints all those subsets whose sum add up to given number. We need to explore the nodes along the breadth and depth of the tree. Generating nodes along breadth is controlled by loop and nodes along the depth are generated using recursion (post order traversal). Pseudo code given below,
if(subset is satisfying the constraint)
print the subset
exclude the current element and consider next element
else
generate the nodes of present level along breadth of tree and
recur for next levels
Following is C implementation of subset sum using variable size tuple vector. Note that the following program explores all possibilities similar to exhaustive search. It is to demonstrate how backtracking can be used. See next code to verify, how we can optimize the backtracking solution.
The power of backtracking appears when we combine explicit and implicit constraints, and we stop generating nodes when these checks fail. We can improve the above algorithm by strengthening the constraint checks and presorting the data. By sorting the initial array, we need not to consider rest of the array, once the sum so far is greater than target number. We can backtrack and check other possibilities.
Similarly, assume the array is presorted and we found one subset. We can generate next node excluding the present node only when inclusion of next node satisfies the constraints. Given below is optimized implementation (it prunes the subtree if it is not satisfying contraints).
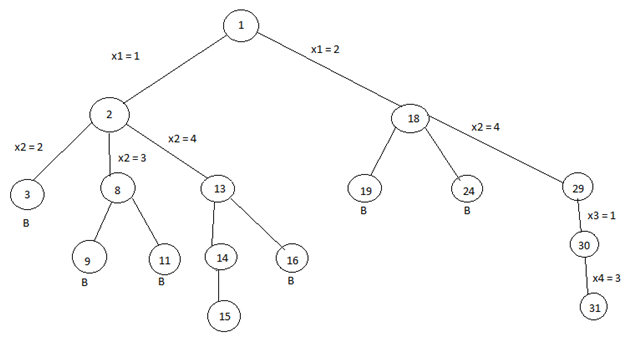
3. Four Queen' problem and solution using backtracking algorithm
In this article, we are going to learn about the 4 Queen's problem and how it can be solved by using backtracking?
Submitted by Shrikant Shejwal, on Dec 29, 2019
Submitted by Shrikant Shejwal, on Dec 29, 2019
4 - Queen's problem
In 4- queens problem, we have 4 queens to be placed on a 4*4 chessboard, satisfying the constraint that no two queens should be in the same row, same column, or in same diagonal.
The solution space according to the external constraints consists of 4 to the power 4, 4-tuples i.e., Si = {1, 2, 3, 4} and 1<= I <=4, whereas according to the internal constraints they consist of 4! solutions i.e., permutation of 4.
Solution of 4 – queen’s with the help of backtracking
We can solve 4-queens problem through backtracking by taking it as a bounding function .in use the criterion that if (x1, x2, ……., xi) is a path to a current E-node, then all the children nodes with parent-child labelings x (i+1) are such that (x1, x2, x3, ….., x(i+1)) represents a chessboard configuration in which no queens are attacking.
So we start with the root node as the only live node. This time this node becomes the E-node and the path is (). We generate the next child. Suppose we are generating the child in ascending order. Thus the node number 2 is generated and path is now 1 i.e., the queen 1 is placed in the first row and in the first column.
Now, node 2 becomes the next E-node or line node. Further, try the next node in the ascending nodes i.e., the node 3 which is having x2 = 2 means queen 2 is placed in the second column but by this the queen 1 and 2 are on the same diagonal, so node 3 becomes dead here so we backtrack it and try the next node which is possible.
Here, the x2 = 3 means the queen 2 is placed in the 3rd column. As it satisfies all the constraints so it becomes the next live node.
After this try for next node 9 having x3 = 2 which means the queen 3 placed in the 2nd column, but by this the 2 and 3 queen are on the same diagonal so it becomes dead. Now we try for next node 11 with x3 = 4, but again the queens 2 and 3 are on the same diagonal so it is also a dead node.

* The B denotes the dead node.
We try for all the possible positions for the queen 3 and if not any position satisfy all the constraints then backtrack to the previous live node.

Now, the node13 become the new live node with x2 = 4, means queen 2 is placed in the 4th column. Move to the next node 14. It becomes the next live node with x3 = 2 means the queen 3 is placed in the 2nd column. Further, we move to the next node 15 with x4 = 3 as the live node. But this makes the queen 3 and 4 on the same diagonal resulting this node 15 is the dead node so we have to backtrack to the node 14 and then backtrack to the node 13 and try the other possible node 16 with x3 = 3 by this also we get the queens 2 and 3 on the same diagonal so the node is the dead node.
So we further backtrack to the node 2 but no other node is left to try so the node 2 is killed so we backtrack to the node 1 and try another sub-tree having x1 = 2 which means queen 1 is placed in the 2nd column.
Now again with the similar reason, nodes 19 and 24 are killed and so we try for the node 29 with x2 = 4 means the queen 2 is placed in the 4th column then we try for the node 30 with x3 = 1 as a live node and finally we proceed to next node 31 with x4 = 3 means the queen 4 is placed in 3rd column.
Here, all the constraints are satisfied, so the desired result for 4 queens is {2, 4, 1, 3}.
8 Queens Problem using Backtracking
Reading time: 30 minutes | Coding time: 10 minutes
You are given an 8x8 chessboard, find a way to place 8 queens such that no queen can attack any other queen on the chessboard. A queen can only be attacked if it lies on the same row, or same column, or the same diagonal of any other queen. Print all the possible configurations.
To solve this problem, we will make use of the Backtracking algorithm. The backtracking algorithm, in general checks all possible configurations and test whether the required result is obtained or not. For thr given problem, we will explore all possible positions the queens can be relatively placed at. The solution will be correct when the number of placed queens = 8.
The time complexity of this approach is O(N!).
Input Format - the number 8, which does not need to be read, but we will take an input number for the sake of generalization of the algorithm to an NxN chessboard.
Output Format - all matrices that constitute the possible solutions will contain the numbers 0(for empty cell) and 1(for a cell where queen is placed). Hence, the output is a set of binary matrices.
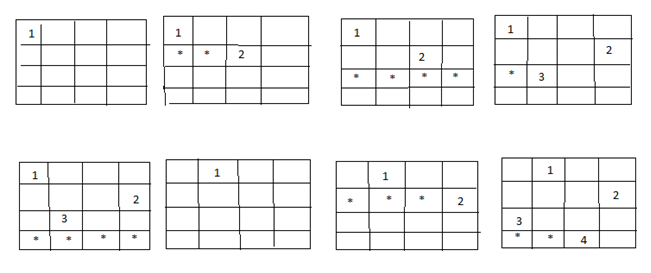
Visualisation from a 4x4 chessboard solution :
In this configuration, we place 2 queens in the first iteration and see that checking by placing further queens is not required as we will not get a solution in this path. Note that in this configuration, all places in the third rows can be attacked.
As the above combination was not possible, we will go back and go for the next iteration. This means we will change the position of the second queen.
In this, we found a solution.
Now let's take a look at the backtracking algorithm and see how it works:
The idea is to place the queens one after the other in columns, and check if previously placed queens cannot attack the current queen we're about to place.
If we find such a row, we return true and put the row and column as part of the solution matrix. If such a column does not exist, we return false and backtrack*
Reading time: 30 minutes | Coding time: 10 minutes
You are given an 8x8 chessboard, find a way to place 8 queens such that no queen can attack any other queen on the chessboard. A queen can only be attacked if it lies on the same row, or same column, or the same diagonal of any other queen. Print all the possible configurations.
To solve this problem, we will make use of the Backtracking algorithm. The backtracking algorithm, in general checks all possible configurations and test whether the required result is obtained or not. For thr given problem, we will explore all possible positions the queens can be relatively placed at. The solution will be correct when the number of placed queens = 8.
The time complexity of this approach is O(N!).
Input Format - the number 8, which does not need to be read, but we will take an input number for the sake of generalization of the algorithm to an NxN chessboard.
Output Format - all matrices that constitute the possible solutions will contain the numbers 0(for empty cell) and 1(for a cell where queen is placed). Hence, the output is a set of binary matrices.
Visualisation from a 4x4 chessboard solution :
In this configuration, we place 2 queens in the first iteration and see that checking by placing further queens is not required as we will not get a solution in this path. Note that in this configuration, all places in the third rows can be attacked.
As the above combination was not possible, we will go back and go for the next iteration. This means we will change the position of the second queen.
In this, we found a solution.
Now let's take a look at the backtracking algorithm and see how it works:
The idea is to place the queens one after the other in columns, and check if previously placed queens cannot attack the current queen we're about to place.
If we find such a row, we return true and put the row and column as part of the solution matrix. If such a column does not exist, we return false and backtrack*
Pseudocode
START
1. begin from the leftmost column
2. if all the queens are placed,
return true/ print configuration
3. check for all rows in the current column
a) if queen placed safely, mark row and column; and
recursively check if we approach in the current
configuration, do we obtain a solution or not
b) if placing yields a solution, return true
c) if placing does not yield a solution, unmark and
try other rows
4. if all rows tried and solution not obtained, return
false and backtrack
END
START
1. begin from the leftmost column
2. if all the queens are placed,
return true/ print configuration
3. check for all rows in the current column
a) if queen placed safely, mark row and column; and
recursively check if we approach in the current
configuration, do we obtain a solution or not
b) if placing yields a solution, return true
c) if placing does not yield a solution, unmark and
try other rows
4. if all rows tried and solution not obtained, return
false and backtrack
END
Implementation
Implementaion of the above backtracking algorithm :
#include <bits/stdc++.h>
using namespace std;
int board[8][8]; // you can pick any matrix size you want
bool isPossible(int n,int row,int col){ // check whether
// placing queen possible or not
// Same Column
for(int i=row-1;i>=0;i--){
if(board[i][col] == 1){
return false;
}
}
//Upper Left Diagonal
for(int i=row-1,j=col-1;i>=0 && j>=0 ; i--,j--){
if(board[i][j] ==1){
return false;
}
}
// Upper Right Diagonal
for(int i=row-1,j=col+1;i>=0 && j<n ; i--,j++){
if(board[i][j] == 1){
return false;
}
}
return true;
}
void nQueenHelper(int n,int row){
if(row==n){
// We have reached some solution.
// Print the board matrix
// return
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cout << board[i][j] << " ";
}
}
cout<<endl;
return;
}
// Place at all possible positions and move to smaller problem
for(int j=0;j<n;j++){
if(isPossible(n,row,j)){ // if no attack, proceed
board[row][j] = 1; // mark row, column with 1
nQueenHelper(n,row+1); // call function to continue
// further
}
board[row][j] = 0; // unmark to backtrack
}
return;
}
void placeNQueens(int n){
memset(board,0,8*8*sizeof(int)); // allocate 8*8 memory
// and initialize all
// cells with zeroes
nQueenHelper(n,0); // call the backtracking function
// and print solutions
}
int main(){
int n;
cin>>n; // could use a default 8 as well
placeNQueens(n);
return 0;
}
Output ( for n = 4): 1 indicates placement of queens
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0
Explanation of the above code solution:
These are two possible solutions from the entire solution set for the 8 queen problem.
main()
{
call placeNQueens(8),
placeNQueens(){
call nQueenHelper(8,0){ row = 0
if(row==n) // won't execute as 0 != 8
for(int j=0; j<8; j++){
{
if(isPossible==true)
{ board[0][0] = 1 // board[row][0] = 1
call nQueenHelper(8,row+1) // recur for all rows further
print matrix when row = 8 if solution obtained
and (row==n) condition is met
}
board[0][0] = 0 // backtrack and try for
// different configurations
}
}
}
}
for example, the following configuration won't be displayed
Implementaion of the above backtracking algorithm :
#include <bits/stdc++.h>
using namespace std;
int board[8][8]; // you can pick any matrix size you want
bool isPossible(int n,int row,int col){ // check whether
// placing queen possible or not
// Same Column
for(int i=row-1;i>=0;i--){
if(board[i][col] == 1){
return false;
}
}
//Upper Left Diagonal
for(int i=row-1,j=col-1;i>=0 && j>=0 ; i--,j--){
if(board[i][j] ==1){
return false;
}
}
// Upper Right Diagonal
for(int i=row-1,j=col+1;i>=0 && j<n ; i--,j++){
if(board[i][j] == 1){
return false;
}
}
return true;
}
void nQueenHelper(int n,int row){
if(row==n){
// We have reached some solution.
// Print the board matrix
// return
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cout << board[i][j] << " ";
}
}
cout<<endl;
return;
}
// Place at all possible positions and move to smaller problem
for(int j=0;j<n;j++){
if(isPossible(n,row,j)){ // if no attack, proceed
board[row][j] = 1; // mark row, column with 1
nQueenHelper(n,row+1); // call function to continue
// further
}
board[row][j] = 0; // unmark to backtrack
}
return;
}
void placeNQueens(int n){
memset(board,0,8*8*sizeof(int)); // allocate 8*8 memory
// and initialize all
// cells with zeroes
nQueenHelper(n,0); // call the backtracking function
// and print solutions
}
int main(){
int n;
cin>>n; // could use a default 8 as well
placeNQueens(n);
return 0;
}
Output ( for n = 4): 1 indicates placement of queens
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0
Explanation of the above code solution:
These are two possible solutions from the entire solution set for the 8 queen problem.
main()
{
call placeNQueens(8),
placeNQueens(){
call nQueenHelper(8,0){ row = 0
if(row==n) // won't execute as 0 != 8
for(int j=0; j<8; j++){
{
if(isPossible==true)
{ board[0][0] = 1 // board[row][0] = 1
call nQueenHelper(8,row+1) // recur for all rows further
print matrix when row = 8 if solution obtained
and (row==n) condition is met
}
board[0][0] = 0 // backtrack and try for
// different configurations
}
}
}
}
for example, the following configuration won't be displayed
Time Complexity Analysis
- the isPossible method takes O(n) time
- for each invocation of loop in nQueenHelper, it runs for O(n) time
- the isPossible condition is present in the loop and also calls nQueenHelper which is recursive
adding this up, the recurrence relation is:
T(n) = O(n^2) + n * T(n-1)
solving the above recurrence by iteration or recursion tree,
the time complexity of the nQueen problem is = O(N!)
- the isPossible method takes O(n) time
- for each invocation of loop in nQueenHelper, it runs for O(n) time
- the isPossible condition is present in the loop and also calls nQueenHelper which is recursive
adding this up, the recurrence relation is:
T(n) = O(n^2) + n * T(n-1)
solving the above recurrence by iteration or recursion tree,
the time complexity of the nQueen problem is = O(N!)
the time complexity of the nQueen problem is = O(N!)
Question :-
You are given an NxN maze with a rat placed at (0,0). Find and print all the paths that the rat can follow to reach its destination i.e (N-1,N-1). The rat can move in all four directions (left,right,up,down).
Value of every cell will be either 0 or 1. 0 represents a blocked cell, the rat cannot move through it, though 1 is an unblocked cell.
Solve the problem using backtracking algorithm,
Input - an integer N and a binary maze of size NxN, showing blocked and
unblocked cells.
Output - all possible path matrices the rat can travel from (0,0) to (N-1,N-1).
Thank you,
Er. Shejwal Shrikant
You are given an NxN maze with a rat placed at (0,0). Find and print all the paths that the rat can follow to reach its destination i.e (N-1,N-1). The rat can move in all four directions (left,right,up,down).
Value of every cell will be either 0 or 1. 0 represents a blocked cell, the rat cannot move through it, though 1 is an unblocked cell.
Solve the problem using backtracking algorithm,
Value of every cell will be either 0 or 1. 0 represents a blocked cell, the rat cannot move through it, though 1 is an unblocked cell.
Solve the problem using backtracking algorithm,
Input - an integer N and a binary maze of size NxN, showing blocked and
unblocked cells.
Output - all possible path matrices the rat can travel from (0,0) to (N-1,N-1).
unblocked cells.
Output - all possible path matrices the rat can travel from (0,0) to (N-1,N-1).
Thank you,
Er. Shejwal Shrikant
Er. Shejwal Shrikant




Comments
Post a Comment