Build a Digit Recognition Model using (SVC)Support Vector Machine Classifier
What is Support Vector Machine?
The objective of the support vector machine algorithm is to find a hyperplane in an N-dimensional space(N — the number of features) that distinctly classifies the data points.


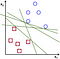
To separate the two classes of data points, there are many possible hyperplanes that could be chosen. Our objective is to find a plane that has the maximum margin, i.e the maximum distance between data points of both classes. Maximizing the margin distance provides some reinforcement so that future data points can be classified with more confidence.
Hyperplanes and Support Vectors

Hyperplanes are decision boundaries that help classify the data points. Data points falling on either side of the hyperplane can be attributed to different classes. Also, the dimension of the hyperplane depends upon the number of features. If the number of input features is 2, then the hyperplane is just a line. If the number of input features is 3, then the hyperplane becomes a two-dimensional plane. It becomes difficult to imagine when the number of features exceeds 3.

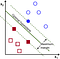
Support vectors are data points that are closer to the hyperplane and influence the position and orientation of the hyperplane. Using these support vectors, we maximize the margin of the classifier. Deleting the support vectors will change the position of the hyperplane. These are the points that help us build our SVM.
Large Margin Intuition
In logistic regression, we take the output of the linear function and squash the value within the range of [0,1] using the sigmoid function. If the squashed value is greater than a threshold value(0.5) we assign it a label 1, else we assign it a label 0. In SVM, we take the output of the linear function and if that output is greater than 1, we identify it with one class and if the output is -1, we identify is with another class. Since the threshold values are changed to 1 and -1 in SVM, we obtain this reinforcement range of values([-1,1]) which acts as margin.
Cost Function and Gradient Updates
In the SVM algorithm, we are looking to maximize the margin between the data points and the hyperplane. The loss function that helps maximize the margin is hinge loss.

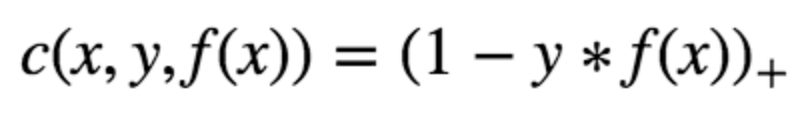
The cost is 0 if the predicted value and the actual value are of the same sign. If they are not, we then calculate the loss value. We also add a regularization parameter the cost function. The objective of the regularization parameter is to balance the margin maximization and loss. After adding the regularization parameter, the cost functions looks as below.

Now that we have the loss function, we take partial derivatives with respect to the weights to find the gradients. Using the gradients, we can update our weights.

When there is no misclassification, i.e our model correctly predicts the class of our data point, we only have to update the gradient from the regularization parameter.

When there is a misclassification, i.e our model make a mistake on the prediction of the class of our data point, we include the loss along with the regularization parameter to perform gradient update.




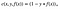
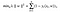
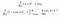
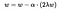
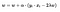
Comments
Post a Comment